Computer Science Intro
How To Avoid Reinventing The Wheel
People think that computer science is the art of geniuses.
But the actual reality is the opposite, just many people doing things that build on each other, like a wall of mini stones.
A History Lesson
"The Mother Of All Demos"
Hardware + software system called "oN-Line System" (NLS)
Mouse-driven windows-based GUI
Video conferencing
Revision control
Collaborative real-time text editor
1968
Presented on December 9th, 1968 by Douglas Engelbert
at Computer Society's Fall Joint Computer Conference in San Francisco
Simula
Classes & Objects
Subclasses and Inheritance
Virtual Procedures (Abstract Methods)
Coroutines (Generators)
Garbage Collection (Automatic Memory Management)
1967
Presented in May 1967 by Ole-Johan Dahl and Kristen Nygaard
at the IFIP Working Conference on simulation languages in Oslo
Wow, that's great!
So, how are we progressing so far?
Computer Science is embarrassed by the computer.
Basic Notions
Building Blocks
Trade-Offs
Multiple algorithms can solve a same problem
Multiple data structures can be used to base these algorithms on
Software development is about trade-offs
-
Processing Speed <=> Memory Consumption
The most comon trade-off that most algorithms and data structures are measured against
Asymptotic Notation
Also known as Bachmann-Landau Notation, or "Big O Notation"
-
f(n) = O(g(n))
"Big O(micron)" — upper bound => worst case
-
f(n) = Ω(g(n))
"Big Omega" — lower bound => best case
-
f(n) = Θ(g(n))
"Big Theta" — upper & lower bound => "average" case
-
Usually abbreviated in Computer Science
i.e. using "O(n)" to state that an algorithm scales linearly

Source: http://bigocheatsheet.com/
Sorting Algorithms
| Algorithm | Time Complexity | Space Complexity | ||
| Best | Average | Worst | Worst | |
| Quicksort | Ω(n log(n)) | Ω(n log(n)) | O(n^2) | O(log(n)) |
|---|---|---|---|---|
| Mergesort | Ω(n log(n)) | Ω(n log(n)) | O(n log(n)) | O(n) |
| Timsort | Ω(n) | Ω(n log(n)) | O(n log(n)) | O(n) |
| Heapsort | Ω(n log(n)) | Ω(n log(n)) | O(n log(n)) | O(1) |
| Bubble Sort | Ω(n) | Θ(n^2) | O(n^2) | O(1) |
| Insertion Sort | Ω(n) | Θ(n^2) | O(n^2) | O(1) |
| Selection Sort | Ω(n^2) | Θ(n^2) | O(n^2) | O(1) |
| Tree Sort | Ω(n log(n)) | Ω(n log(n)) | O(n^2) | O(n) |
| Shell Sort | Ω(n log(n)) | Θ(n(log(n))^2) | O(n(log(n))^2) | O(1) |
| Bucket Sort | Ω(n+k) | Θ(n+k) | O(n^2) | O(n) |
| Radix Sort | Ω(nk) | Θ(nk) | O(nk) | O(n+k) |
| Counting Sort | Ω(n+k) | Θ(n+k) | O(n+k) | O(k) |
| Cubesort | Ω(n) | Ω(n log(n)) | O(n log(n)) | O(n) |
Source: http://bigocheatsheet.com/
Data Structures
| Data Structure | Time Complexity | Space Complexity | |||||||
| Average | Worst | Worst | |||||||
| Access | Search | Insertion | Deletion | Access | Search | Insertion | Deletion | ||
| Array | Θ(1) | Θ(n) | Θ(n) | Θ(n) | O(1) | O(n) | O(n) | O(n) | O(n) |
|---|---|---|---|---|---|---|---|---|---|
| Stack | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Queue | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Single-Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Double-Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Skip List | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n log(n)) |
| Hash Table | N/A | Θ(1) | Θ(1) | Θ(1) | N/A | O(n) | O(n) | O(n) | O(n) |
| Binary Search Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
| Cartesian Tree | N/A | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | N/A | O(n) | O(n) | O(n) | O(n) |
| B-Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Red-Black Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Splay Tree | N/A | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | N/A | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| AVL Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| KD Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
Source: http://bigocheatsheet.com/
Most Problems Have Been Solved Decades Ago
How To Solve Problems
Assume: Someone had that same problem before you
Name your problem
Find the algorithm that solves your problem
Find an implementation of the algorithm that fits your environment
Algorithm Naming
Mostly harmless
Mostly
harmlessMostly useless!
-
Non-memorable Names of Author(s)
"Steinhaus–Johnson–Trotter Algorithm"
-
Ridiculous Acronym
"RIPEMD-160"
-
Ludicrous Combination of Both
"Cooley–Tukey FFT Algorithm"
Ok, there are exceptions to these as well.
Finding Algorithms
-
Search for what you think the solution might be called
Example: "Text Pattern Recognition"
-
Search for how you would describe the problem to solve
Example: "Discover recurring patterns in clusters of text"
-
Browse categorized overviews
Example: List of algorithms on Wikipedia
-
Use visual maps and flow charts
Example: Map of Data Mining Algorithms
Practical Example
WP-CLI suggestions after typo
The Problem

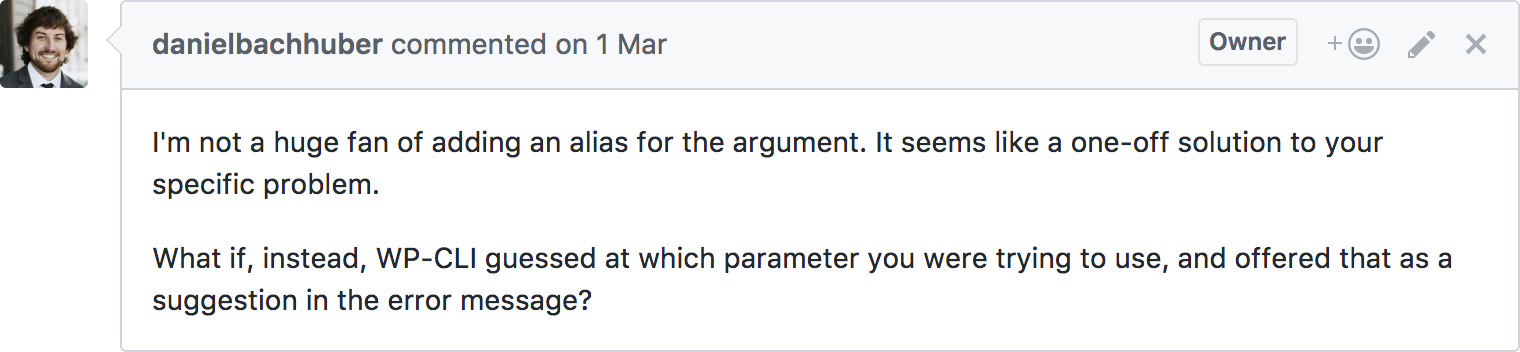
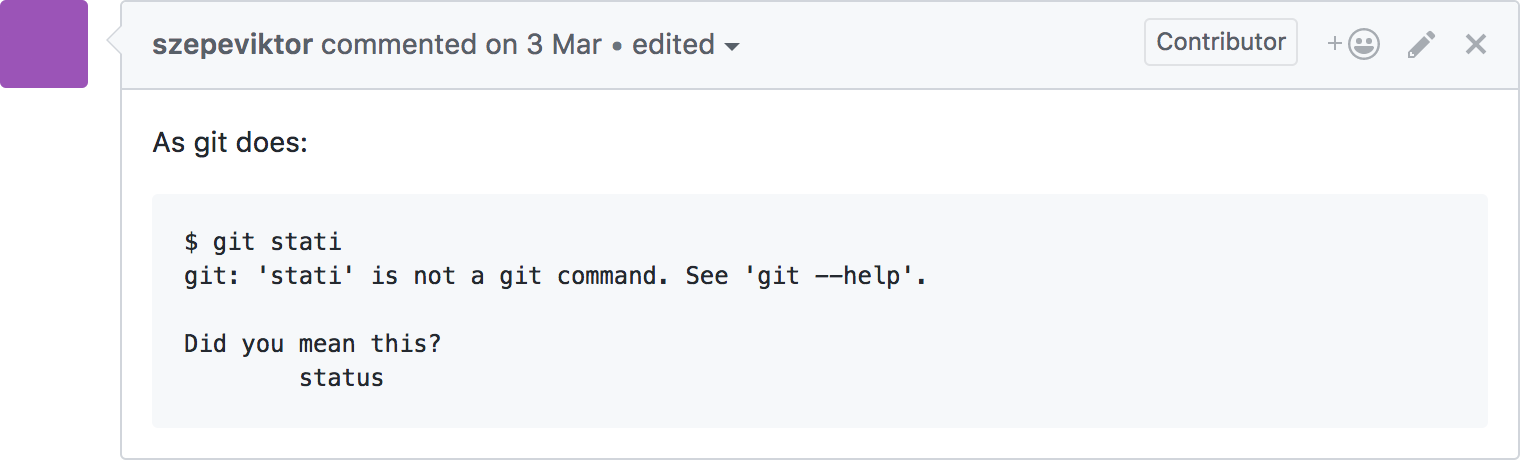
Game On!
Search for an Algorithm (1/4)
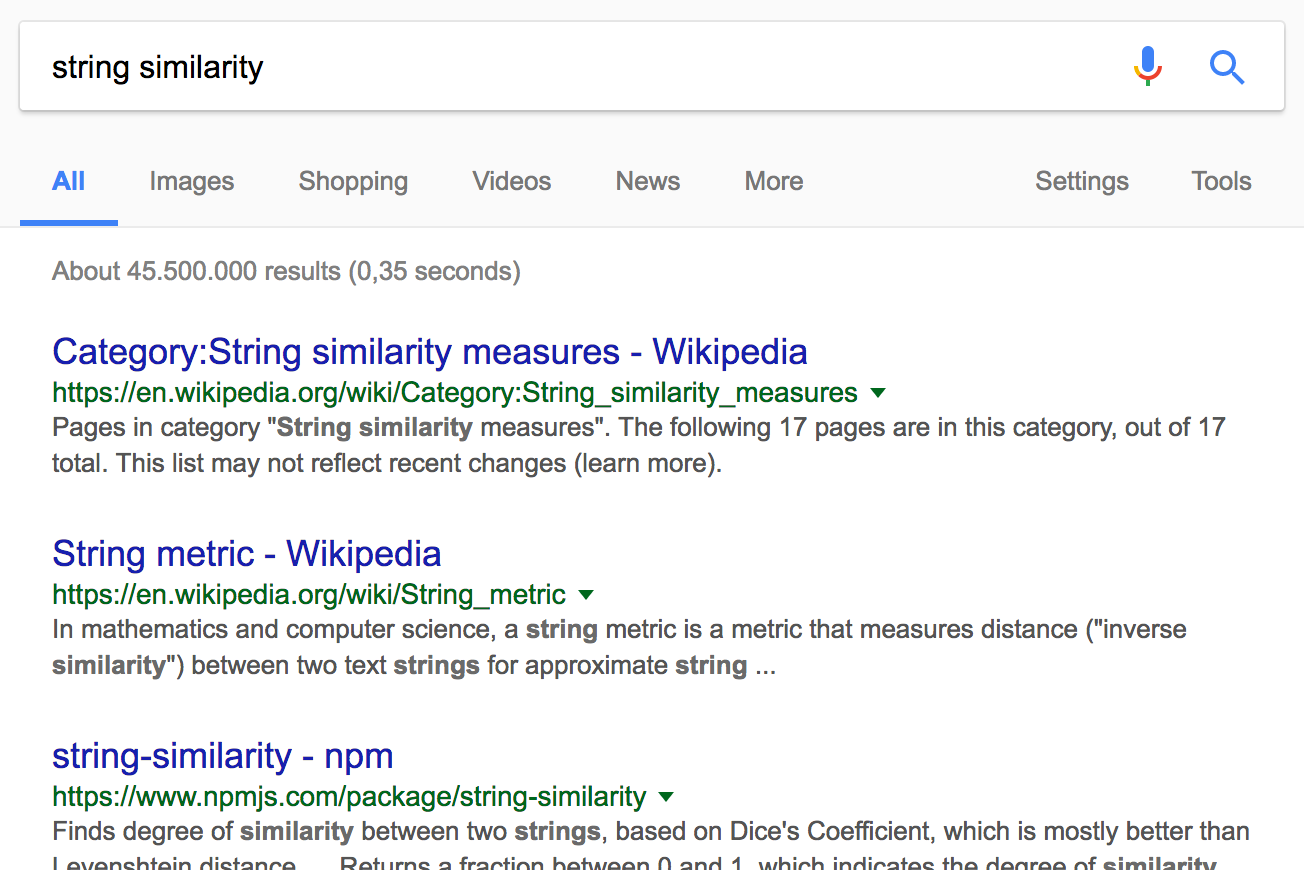
Think of a combination of nouns that describes the approach
For the problem at hand: In a list of known arguments, find the one most similar to the user entry
=> "String Similarity"
Search for an Algorithm (2/4)
Search for an Algorithm (3/4)

Search for an Algorithm (4/4)
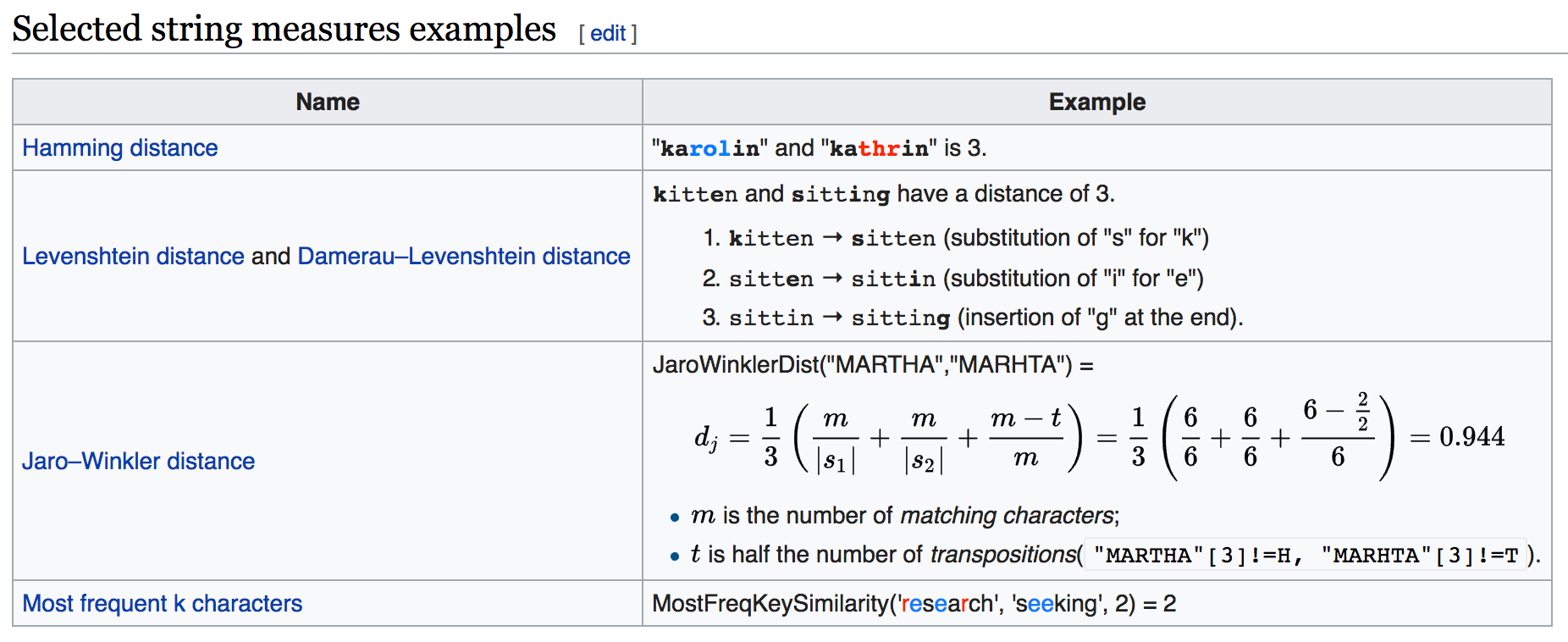
Levenshtein Distance
In information theory, Linguistics and computer science, the Levenshtein distance is a string metric for measuring the difference between two sequences.
Informally, the Levenshtein distance between two words is the minimum number of single-character edits (insertions, deletions or substitutions) required to change one word into the other.
It is named after Vladimir Levenshtein, who considered this distance in 1965.
Levenshtein Distance
Definition
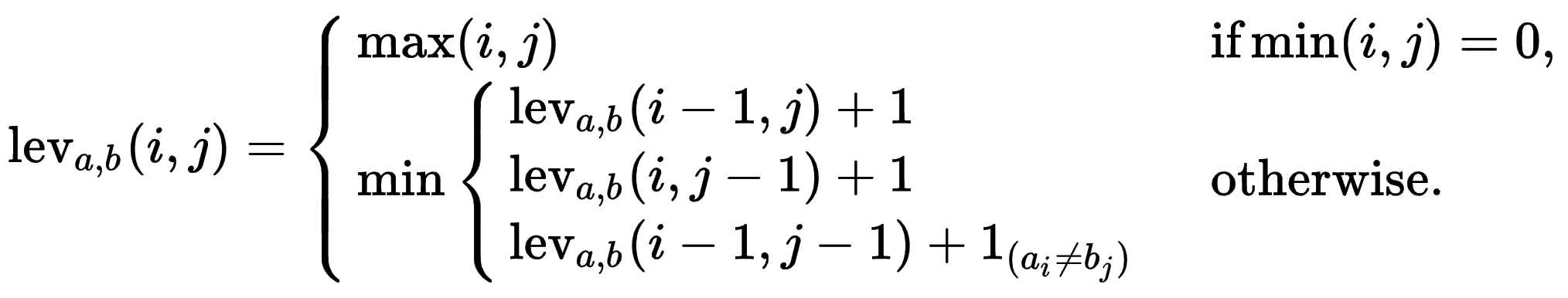
Levenshtein Distance
Recursive Implementation in C
// len_s and len_t are the number of characters in string s and t respectively
int LevenshteinDistance(const char *s, int len_s, const char *t, int len_t)
{
int cost;
/* base case: empty strings */
if (len_s == 0) return len_t;
if (len_t == 0) return len_s;
/* test if last characters of the strings match */
if (s[len_s-1] == t[len_t-1])
cost = 0;
else
cost = 1;
/* return minimum of delete char from s, delete char from t, and delete char from both */
return minimum(LevenshteinDistance(s, len_s - 1, t, len_t ) + 1,
LevenshteinDistance(s, len_s , t, len_t - 1) + 1,
LevenshteinDistance(s, len_s - 1, t, len_t - 1) + cost);
}
Levenshtein Distance
Iterative Pseudocode Using Dynamic Programming
function LevenshteinDistance(char s[1..m], char t[1..n]):
declare int v0[n + 1]
declare int v1[n + 1]
for i from 0 to n:
v0[i] = i
for i from 0 to m-1:
v1[0] = i + 1
for j from 0 to n-1:
if s[i] = t[j]:
substitutionCost := 0
else:
substitutionCost := 1
v1[j + 1] := minimum(v1[j] + 1, v0[j + 1] + 1, v0[j] + substitutionCost)
swap v0 with v1
return v0[n]
Search for PHP Implementation (1/2)
Search for PHP Implementation (2/2)
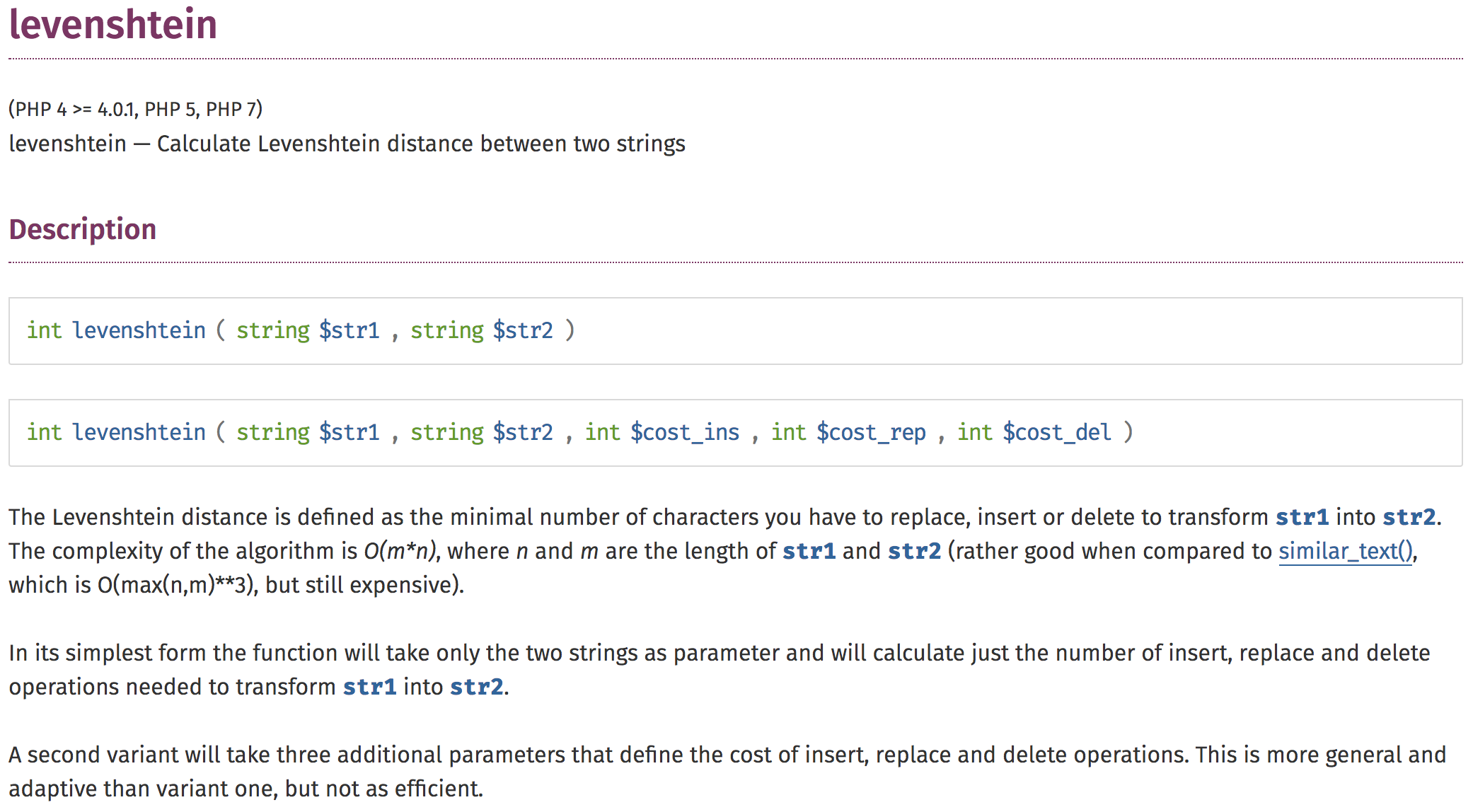
WP-CLI Implementation
function get_suggestion( $target, array $options, $threshold = 2 ) {
if ( empty( $options ) ) {
return '';
}
// Calculate distances from each of known command strings to user entry.
foreach ( $options as $option ) {
$distance = levenshtein( $option, $target );
$levenshtein[ $option ] = $distance;
}
// Sort known command strings by distance to user entry.
asort( $levenshtein );
// Fetch the closest command string.
reset( $levenshtein );
$suggestion = key( $levenshtein );
// Only return a suggestion if below a given threshold.
return $levenshtein[ $suggestion ] <= $threshold && $suggestion !== $target
? (string) $suggestion
: '';
}
What's Next ?
Free Online Courses
Study Guide
Questions ?
I'm Alain Schlesser.
Follow me on Twitter:
@schlesseraOr visit my Personal Blog:
www.alainschlesser.com